Basics of Data Acquisition
This general application note is an introduction to data acquisition to help to ensure the best results when recording with an e-corder system. (Its text is included in recent Chart and Scope users guides.)
Contents
Introduction
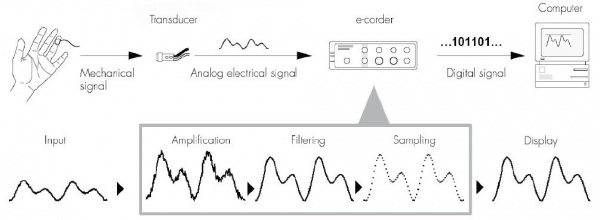
The purpose of the e-corder system is to acquire, store, analyze and display data. Figure 1 summarizes the acquisition. Usually, the raw input signal is in the form of an analog voltage whose amplitude varies continuously over time. This voltage is monitored by the hardware, which can modify it by amplification and filtering processes called ‘signal conditioning’. Signal conditioning may also include zeroing, for example the removal of an unwanted steady offset voltage from a transducer’s output. After signal conditioning, the analog voltage is sampled at regular intervals. The signal is then converted from analog to digital form before transmission to the attached computer (computers need digital data). The computer software usually displays the data directly; it plots the sampled and digitized data points and reconstructs the original waveform by drawing lines between the points. Digital data can be stored on disk for later retrieval. Software can also easily manipulate and analyze the data in a wide variety of ways.
Most of the parameters that affect acquisition can be set by the user through the software. To make a good recording, the parameters must be appropriate for the signals being recorded. In some disciplines you may be able to find tables of suggested sampling rates, ranges, and filter settings, but these should not be applied blindly. You still need to know the science (what you are recording, why you are recording it, and what relation it bears to real phenomena) and the technique (how best to record, and what limitations or compromises are inherent in the process).
Sampling Rate
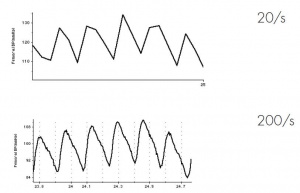
Sampling replaces the original continuous analog signal by a series of discrete values (samples) taken at regular time intervals. The appropriate sampling rate depends on the signal to be measured. If the sampling rate is too low, information is irreversibly lost and the original signal will not be represented correctly; this is shown in Figure 2. If it is too high, there is no loss of information, but the excess data increases processing time and results in unnecessarily large disk files.
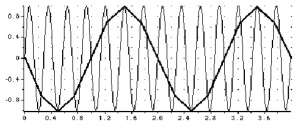
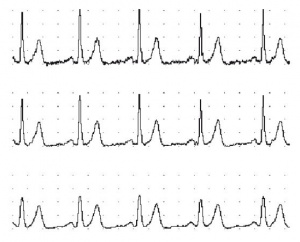
Recordings of periodic waveforms that have been sampled too slowly may be misleading as well as inaccurate because of aliasing, as shown in Figure 3. An analogy to aliasing can be seen in old films: spoked wagon wheels may appear to stop or even go backwards when their rate of rotation matches the film frame speed — obviously not an accurate record.
To prevent aliasing, the sampling rate must be at least twice the rate of the highest expected frequency of the incoming waveform. This sampling rate is known as the Nyquist frequency, the minimum rate at which digital sampling can accurately record an analog signal. For example, if a signal has maximum frequency components of 100 Hz, the sampling rate needs to be at least 200 Hz to record it accurately. To provide a safety factor to guard against information loss, it is usual to sample at five to ten times the highest expected frequency rather than the minimum two times.
In most cases, the highest expected frequency will be known. It may well be limited by the transducer used: a bridge transducer to measure mechanical force will not produce high frequencies, for instance. If you are unsure of the frequency range (bandwidth) of your signal, a useful rule of thumb is to choose a sampling rate high enough to allow at least 5 to 20 samples for any transient peaks or recurring waves in the signal.
The highest frequencies in a signal can be formally determined by sampling the signal at the maximum rate, and looking at the spectrum of the signal (using the Spectrum window). High-frequency components in the spectrum with less than 2% or so of maximum amplitude usually contribute little to recording accuracy.
Filtering
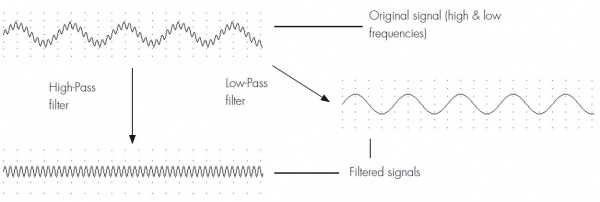
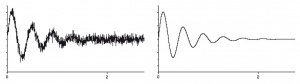
Any analog waveform can be described mathematically as the sum of a number of pure sine waves at various frequencies and amplitudes. Low frequencies characterize the slowly changing parts of a waveform; high frequencies, the quickly changing parts. A filter removes selected frequencies from a signal: for instance, a low-pass filter lets low frequencies pass and stops high frequencies. Low-pass filters are commonly used to help reduce noise and give a smoother signal. A high-pass filter removes any steady component of a signal; it also removes slow fluctuations; see Figure 4.
Filters are imperfect. A 200 Hz low-pass analog filter, say, might leave frequencies up to 150 Hz untouched, reduce a 200 Hz signal to 0.7 of its original amplitude (this is its cut-off frequency), and reduce higher frequencies more and more. If you were expecting useful frequencies of up to 100 Hz, you could sample at 400 samples per second and filter out any higher frequencies using a 200 Hz filter. If higher frequencies are left unfiltered, then they could possibly be aliased, resulting in the false appearance of lower frequencies.
Filtering can change the signal to some extent: its use must be balanced against the distortions it can remove, such as noise, baseline drift, and aliasing. If the filter settings overlap the bandwidth of a signal, then the signal will have components removed. If you were interested in a waveform with components down to 5 Hz and used a 20 Hz high-pass filter (filtering out 0 to 20 Hz signals), then vital information would be lost from the signal. This is shown in Figure 5.
Digitization
When analog data such as voltage amplitude is converted to digital form for use by a computer, it must conform to a fixed number of values (for instance, a digital thermometer might only measure temperature to the nearest degree). Any analog values between these values are rounded up or down. The approximation is usually very good, since the number of values is very large. The analog-to-digital converters (ADCs) that perform the digitization usually generate a number of values equal to a power of two: an ADC with 12-bit resolution can resolve a signal into 212 or 4096 possible amplitude values; an ADC with 16-bit resolution can resolve a signal into 216 or 65 536 possible amplitude values.
e-corder units use a 16-bit ADC. Chart 5 fits 64 000 of the 65 536 values to the range, allowing some overrange for signal extremes. The values in a 10 V range, say, would be divided into 64 000 fixed values from –10 V to +10 V; the minimum change in voltage that could be discerned at that range would be 0.3125 mV. At 10 mV range, the minimum discernible voltage change would be 0.3125 µV.
Range
Range is inversely proportional to gain, the amount of amplification, and is a more useful concept than gain since it relates directly to the signal being measured. The range can be set independently for each input on a e-corder recording unit.
If the signal amplitude exceeds the range, there will be severe loss of information. (This is the same as ‘clipping’ in a stereo system where music is severely distorted when the amplitude exceeds the capabilities of the amplifier.) Any signal exceeding the range is ‘out of range’, a condition indicated where no amplitude can be given. If there is any possibility of this condition occurring, you should set the range to a larger value.
For the best resolution, the maximum amplitude of the signal you are interested in should be reasonably close to the chosen range without exceeding it. That way, the minimum change in voltage discernible in digitization remains small in relation to the signal being measured (the signal is digitized after it is amplified). If a signal is very small in relation to the range, then its resolution will be degraded. In extreme cases, the recorded waveform may appear stepped rather than smooth. Even though you could see a ±380 mV signal easily enough at the default 10 V range, you would use the 500 mV range to measure it at maximum resolution. It would be safer in practice to use a 1 V or 2 V range, though, since unexpectedly large peaks could exceed the 500 mV range if the signal was not well-behaved. Changing the display of the waveform on screen (by enlarging it in the Zoom View or by stretching or shrinking its Amplitude axis, for instance) does not affect its resolution, just its appearance.
Noise
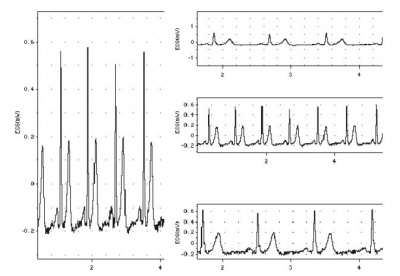
Noise is defined as ‘unwanted signal’. It is likely to be a problem at lower range settings, when you are trying to measure very small signals. Random noise, such as thermal noise, is inherent in all electronic circuits, including those of the e-corder recording unit, and generally must be filtered to minimize it. The trick is to choose a low-pass filter setting that removes most of the background noise without unduly changing the signal of interest. See Figure 6.
Differential inputs can reduce common-mode noise due to ground loops. (Ground loops occur where multiple connected pieces of recording equipment are connected to mains power grounds.) e-corder single-sided inputs are ‘quasi-differential’, and automatically neutralize up to a several volts of ground loop noise.
Reasonable care in the arrangement and shielding of equipment and cables will reduce signal interference from unshielded power lines, switching equipment, fluorescent tubes, transformers, computers, network cables, VDUs, and so on.
Display and Expectations
The two most important settings for data recording are the input range and recording speed. Provided these are set correctly, then your signals will be recorded which high precision. However, the actual appearance of the data on the computer monitor can be affected by the vertical magnification and time base compression used in the Chart display settings, and screen resolution of your monitor, as shown in Figure 7.
The screen display on a monitor is generally about 72 dots per inch (dpi), so the apparent resolution may be poor if the display is kept small. However, the resolution of the underlying recorded data is independent of the resolution of the display: even if the channel is very thin or not visible on screen, sampled data are recorded at full fidelity, as can be seen by expanding the channel display or examining the signal in the Zoom window.
High-resolution printing will also show data more accurately.
It is important to check display settings and axis labels carefully when examining a signal.